1. Algorithms and Computation
- Se define como f(x) = I → O
- I: Input
- O: Output
- Se define un problema de cómo se puede crear un algoritmo para encontrar a 2 alumnos que estén de cumpleaños el mismo día.
- Para probar que el algoritmo que definimos se usa Inductive hypothesis1
Inductive proof
- Sirve para probar que nuestro algoritmo es correcto teoricamente.
Mathematical induction is a method for proving that a statement P(n)
is true for every natural number n
, that is, that the infinitely many cases P(0),P(1),P(2),P(3),…
all hold. (Wikipedia)
- Para usar inducción matemática necesitamos 2 proposiciones: Un proposición base que prueba P_1 (n=0 por ejemplo caso inicial) es verdader. La segunda proposición “Paso inductivo”, necesitamos para todas las proposiciones n= k, entonces tiene que ser verdad para el n= k +1. La demostración de ambas concluimos que es real para todos los numeros naturales.
Desarrollo del ejercicio
- Problema: se define cómo se puede crear un algoritmo para encontrar a 2 alumnos que estén de cumpleaños el mismo día.
- Siguiendo el ejercicio, se define como hipotesis inductiva: si los primeros K students tienen un match, el algoritmo retorna el match antes de entrevistar al estudiante K+1. (En otras palabras eso significa que alcanzo a encontrar un match antes que terminará el listado de estudiantes)
- Se define un base case en el cual es 0. Es decir que los primeros 0 estudiantes no tienen un match.
- La idea de usar inducción es para aislar el problema en pequeños problemas.
- Entonces se asume que para k = k’
-
- Si k’ contiene un match → ya esta probado por la inducción
- Si K’+1 contiene un match, el algoritmo revisa todas las posibilidades de todos los estudiantes (por fuerza bruta, ya que revisó todos los alumnos).
-
Efficiency
- No se mide el tiempo, solamente la cantidad de operaciones (fundamentals operations or ops).
- Se espera que el performance dependa del tamaño de nuestro input.
- O(1) = constante
- O(log n) = Logarithmic time
- almost good as a consta nt.
- O(N) = linear
- O(n log n) = linear logarithmic
- O(n2) = exponencial
2. Data Structures and Dynamic Arrays
| Interface (API) | Data Structure |
|---|---|
| Says what you want to do | How you do it |
| What data you can store | How to to store it. |
| Specification of what to do | Representation of data |
| What operations supported | What algorithms are supported for those operations |
| Problems | Solutions to the problem |
Interfaces for this class
- Set
- Sequence
- Representa una secuencia en particular. Ejemplo un array: [5,4,3,5]
Static Sequence Problem
Interface
- DS significa data structure
- n items, x_0 , x_1, x_n-1
- build(x): make new DS for items in X
- len(): return n
- iter_sequence: output x0, x1. Outputs the sequence in the order.
- get_at(i): return x_i given index
- set_at(i,x): set x_i to x
- get first/last(): consiguie le primer valor o el ultimo valor de un array
- set first/last(x):
Solution - Static Array
- Static Array
- RAM: Random access memory.
- w: machine word size. 64 bits.
- RAM Memory = array of w-bit words
- Array significa secuencias de memoria.
- array(i) = RAM Memory(address (array) + i)
- Complejijdad
- get_at/set_at or len en complejidad es O(1)
- build / iter_seq es complejijdad O(N)
- Como se construye un array:
- Memory allocation model: puedes crear un array de tamaño n, en un tiempo O(n).
- El espacio que usa es el tiempo que toma en crearse.
- space = O(time)
Dynamic Sequence Interface
Javascript o Python son lenguajes que usan dynamic arrays.
Interface
- insert_at(i,x): hace que X sea el nuevo X_i, haciendo que se muevan consecutivamente los indices de los items que van después (shifting). x_i → x_i+1 -x_i+2 → … → x_n-i
- delete at (i): elimina x_i, haciendo que se muevan los indices de los que van después. xi ← x+i ←… ← x_n’-1
- insert /delete first/last (x) / ( )
- insert:
- insert first: agrega un valor al inicio y modifica los valores siguientesl
- insert last: agrega un valor al final sin modificar los indices.
- delete first/last: elimina el primer o ultimo
- delete first: elimina el primero y modifica los valores siguientes
- delete last: elimina el último valor sin modificar los indices.
- De primera se puede pensar que estos metodos no son mas que lo mismo que un insert o delete_at, estos casos en especial se pueden resolver de una manera más rápida. Ver 20:26
- delete first/last: elimina el primer o ultimo
Solution
Hay 2 posibles soluciones:
Static Array
- Si usamos insert first, eso significa que tenemos que mover todos los indices de los siguientes valores. Es una operacion costosa.
- Complejidad: O(n)
- shifting: si estamos cerca del inicio, eso significa que tenemos que hacer shifiting.
- allocation / copying: tenemos que copiar el array para poder mover los indices.
- Bad for dynamic operations.
Linked List
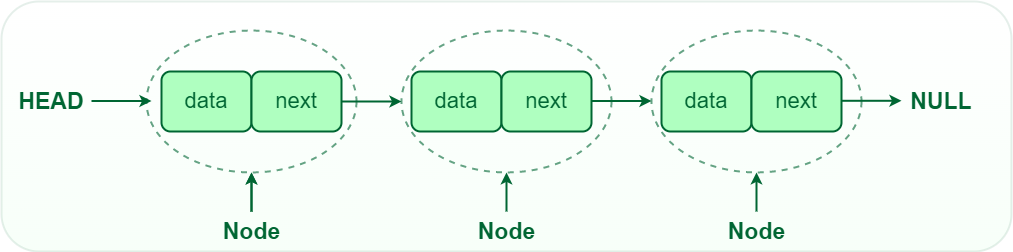
- Pointer based structure
- Store items in nodes. Each item store an item(item), and its index that points to the next sequence. (pointer)
- Each pointer gives the structure.
- Pointers son solamente indices que indican donde esta el item en memoria.
- El inicio de una linked list se indica por el HEAD que es un pointer que apunta al inicio. Tiene un metodo length(), y también puede augmentarse para que tenga un TAIL indicando el último elemento
- Las operaciones de insert_first /delete first son más eficientes que un array normal. O(1) Ya que para cambiar el primer item, solamente hay que cambiar el HEAD Pointer al nuevo item que insertamos.
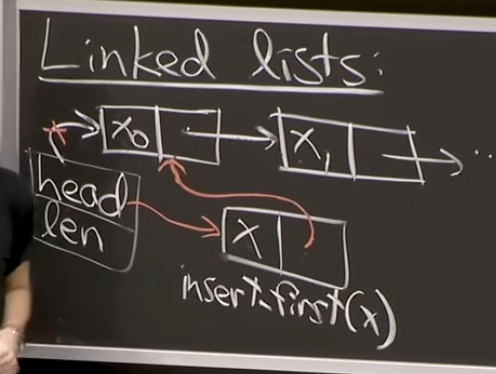
- get / set_at son O(i) complejidad. En el peor caso es O(n). Ya que para conocer el item en una posicion i (digamos 10) hay que recorrer toda la linked list, siguiendo puntero por puntero.
- get_last puede ser O(1) si es que existe un TAIL que tenga un pointer al último elemento de la linked list.
- En la realidad los linked list estan en un array en memoria.
How Python implements Dynamic Arrays so called List
- n = el numero de items en la secuencia.
- Definimos el constraint que el size del array = n
- size of array = O(n) or some constants time N (10n, 25n)
Footnotes
-
Revisar proofs ↩